ペンギンデータセットでデータサイエンス入門 〜 教師なし学習・主成分分析編【Python/scikit-learn/機械学習】
目次
こんにちは。
さて、昨今データサイエンス入門者に爆発的な人気を誇っているpalmerpenguinsなるペンギンデータセット。このブログではこちらの記事で紹介しているように、ペンギンデータセットを使って基本的な機械学習についてわかりやすくまとめています。
今回はペンギンデータセットを使って主成分分析について学習・実践してみましょう。
という初心者向けの記事です。
よろしく。
この記事を読めば、多数の特徴量(変数)をもつデータセットを、より少ない軸で分類する簡単なモデルを作成できるようになります。
ちなみに本記事ではプログラムにPython3と、機械学習ライブラリにscikit-learnを使います。
過去の関連記事はこちらです。
- ペンギンデータセットで機械学習/データサイエンスをはじめよう〜ダウンロード編
- ペンギンデータセットでデータエンジニアリングの基礎を学ぼう
- ペンギンデータセットでデータサイエンス入門 〜 特徴行列の可視化編
- ペンギンデータセットでデータサイエンス入門 〜 機械学習の基本 教師あり学習・単回帰編
- ペンギンデータセットでデータサイエンス入門 〜 教師あり学習・分類編
【目的と概要】主成分分析とは?
今回やりたいことは、「ペンギンの種類を区別するための指標として4つの特徴を測ってみたけど、4次元にプロットするのはわかりにくいから、種類の違いをよく反映している2つくらいの軸を作って2次元にプロットしてみたい」という問題に取り組むことです。
機械学習のカテゴリでいうと、「教師なし学習」に分類されます。
教師なし学習とは、Wikipediaによると「データの背後に存在する本質的な構造を抽出するために用いられる」とのことです。教師ありのように予め答えがわかるデータを学習させて未知のデータを予測したり分類したりするのではなく、答えはわからないけど今あるデータの特徴を使って何らかの価値を生み出そうとする行為となります。
要は、先程書いた「今回やりたいこと」って、「種類の違いをよく反映している2つの軸」が何かわかっていれば、苦労しないで最初からそのデータを集められますよね。その特徴的な軸を探すのが大変なので、すでにあるデータから計算で求めましょう、ということです。この求めたい2つの軸が、「主成分」と呼ばれるものです。
よく用いられる身近な例えが、「身長」と「体重」という2軸の代わりに、「BMI」で評価するという例。これも2つの軸から1つの軸を取り出すという意味で、主成分分析みたいなものです。
主成分分析と似たような意味の言葉で「次元削減」というものがありますが、「主成分分析」は「次元削減」の手法のひとつです。
【準備】データセットの準備
まずは今回使うデータセットをインポートします。教師あり学習・分類編と同じです。
import pandas as pd
df = pd.read_csv('penguins.csv')
use_col = [
'species',
'bill_length_mm',
'bill_depth_mm',
'flipper_length_mm',
'body_mass_g',
]
df = df[use_col].rename(columns={
'bill_length_mm':'bill_length',
'bill_depth_mm':'bill_depth',
'flipper_length_mm':'flipper_length',
'body_mass_g':'body_mass'
})
こんな感じのデータになります。
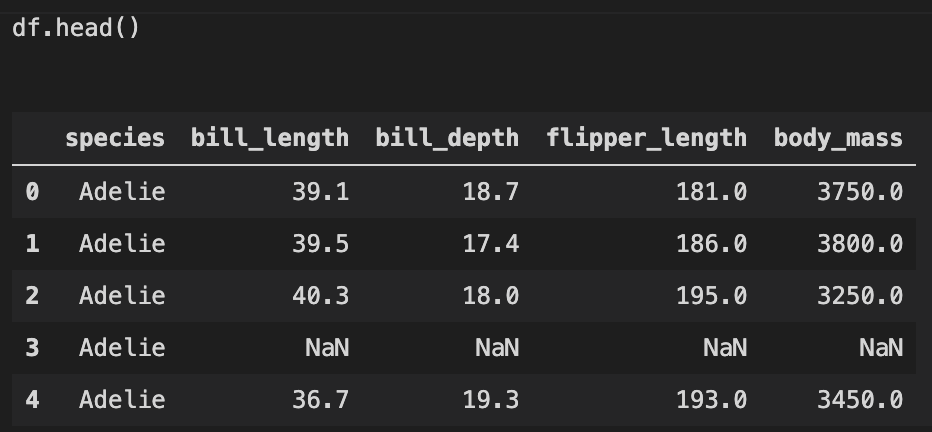
NaN値は除外してクレンジングします。
df = df[~df.isnull().any(axis=1)] # NaNがひとつでもある行を削除
342 rows × 5 columnsになりました。
【おさらい】scikit-learnを使った機械学習の手順
さて、前回までの記事でscikit-learnの機械学習の流れは以下の通りでしたが、今回もほぼ同じです。
- モデル選択
- モデルのインスタンス化とハイパーパラメータの選択
- 特徴行列と目的配列の設定
- フィッティング
今まではフィッティングの後に未知のデータを予測していましたが、今回は新たに作成した軸でプロットしてみます。
- 可視化
それでは順番に見ていきましょう。
【本編】主成分分析してみる
上記の流れに沿ってプログラムを実行していきます。
1. モデル選択
主成分分析用のモデルPCAをインポートします。
from sklearn.decomposition import PCA
参考ドキュメント : scikit-learn | sklearn.decomposition.PCA
ちなみにdecompositionとは「分解」という意味で、PCAは、Principal Component Analysisということで、主成分分析のことです。
2. モデルのインスタンス化とハイパーパラメータの選択
今回は2軸を選択したいので、n_componentsに2をセットします。
pca = PCA(n_components=2)
3. 特徴行列と目的配列の設定
y = df.species
X = df.drop('species', axis=1)
yは、ペンギンの種類、Xは、ペンギンのくちばしの長さ、くちばしの太さ、羽の長さ、体重という4次元の特徴量です。
4. フィッティング
pca.fit(X)
以上。
5. 可視化
先程のフィッティングで軸を作ったので、この軸にXを変換して、その軸についてプロットする、という流れです。
軸の変換はtransformというメソッドがあるので、これにXを入力します。
X_2D = pca.transform(X)
次に、出来上がった軸をそれぞれ元のデータフレームの新しい列として追加します。
df['PCA1'] = X_2D[:,0]
df['PCA2'] = X_2D[:,1]
データフレームの可視化なのでseabornが便利です。
hueはプロットを色分け分類できるので、今回はspeciesを設定してペンギンの種類が区別できそうかを見てみます。
import seaborn as sns
sns.lmplot('PCA1','PCA2',hue='species',data=df,fit_reg=False)
参考ドキュメント : seaborn | seaborn.lmplot
結果↓
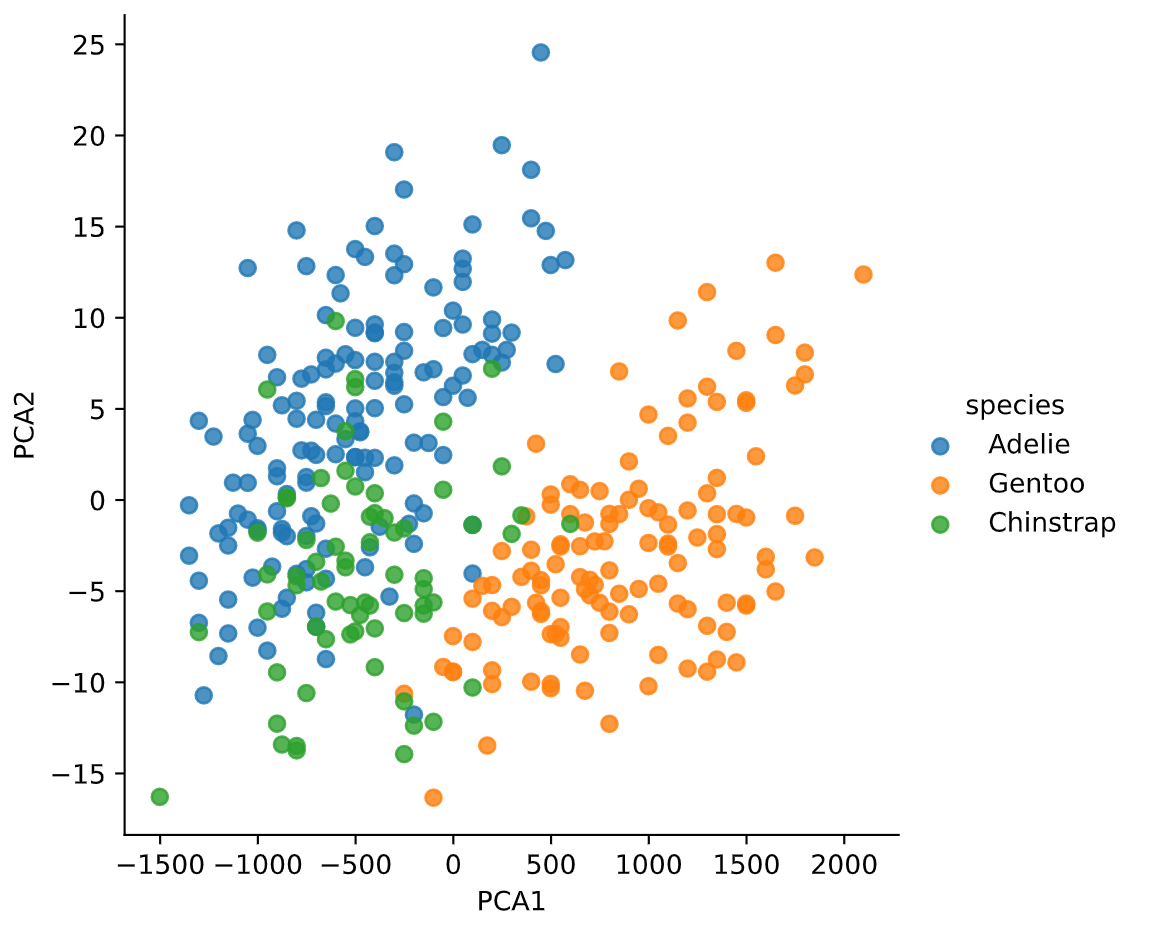
3種類が塊となって2次元にプロットできていそうです。少し緑(ヒゲペンギン)と青(アデリーペンギン)が混ざりすぎな気もしますが...
ということで、元々のデータは4つの特徴量の4次元データでしたが、2次元でもそこそこ種類が区別できる形にプロットできました。
逆に言うと、選択した4次元の特徴量からでは、2次元で綺麗に分類することは難しそう、とも解釈できます。少なくとも第一主成分PCA1だけでは、ジェンツーペンギン(橙)はそこそこ特徴をつかめてそうですが、他の2種類は完全に混ざりそうですよね。第二主成分PCA2まであって、やっとヒゲペンギンとアデリーペンギンの違いが見えてきた、という感じがします。
【原理と解釈】結局、主成分分析とは何をしていたのか。
いつも通り単純な数行のプログラムで主成分分析ができることはわかりましたが、結局何をしているのかがわかりにくいので、今回は少し深堀りしてみようと思います。
ポイントは以下の通りです。
- 第一主成分は、全ての特徴量に対し最も分散(ばらつき)が大きくなる軸
- つまり、なるべく元の情報を失わないように軸を選ぶ。
- 第二主成分は、第一主成分に対し直交する軸で、かつ最も分散が大きくなる軸
- つまり、第一主成分で失われた情報を補う。
- 以降、第三・第四も同様に直交する軸から探していく。
Wikipedia(主成分分析)にあった図のイメージがわかりやすいです。データのばらつきが最も説明できる直交する2軸を新しく作っています。
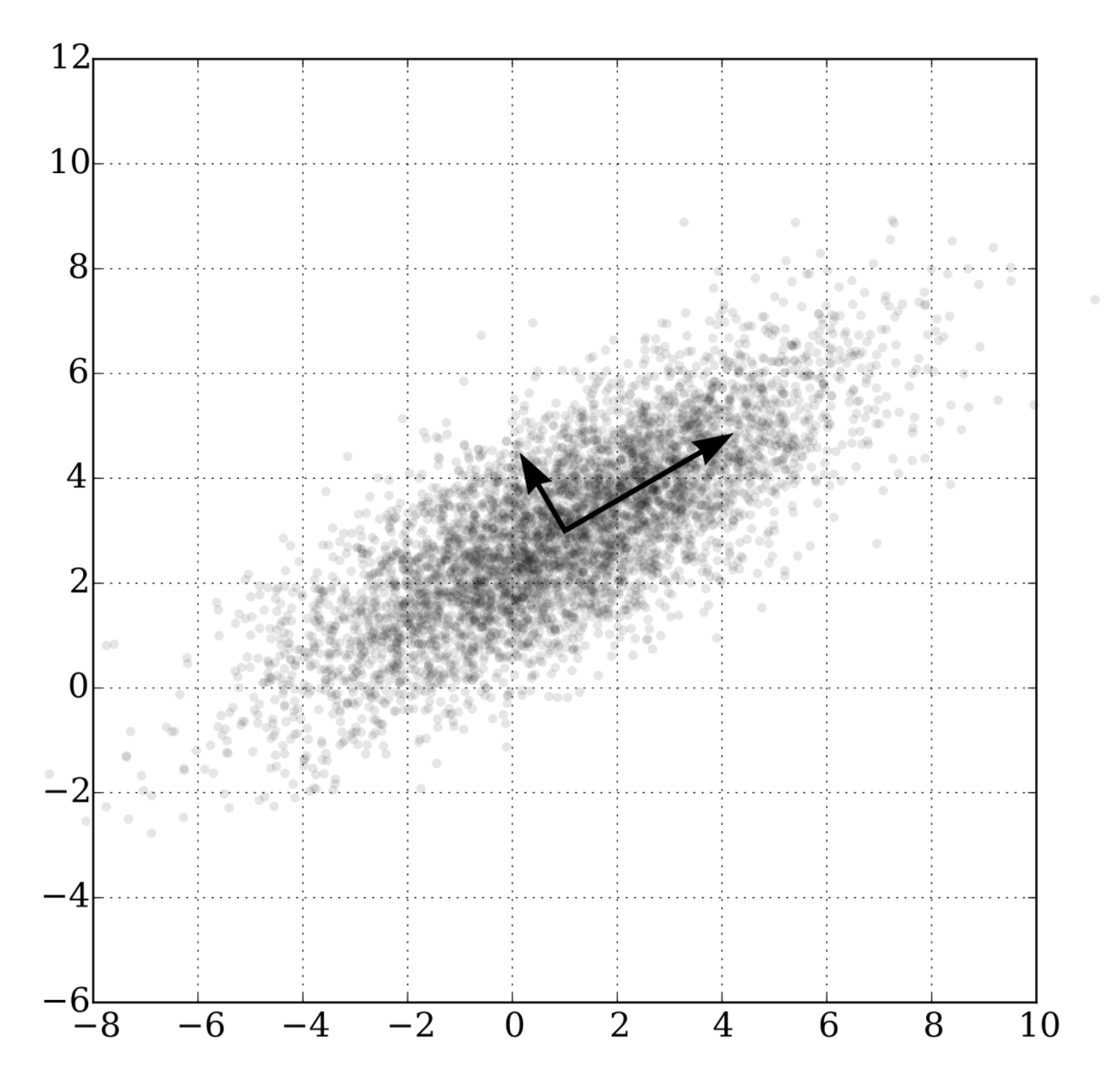
で、数学的にこれを内部で何やってるかというと、特異値分解です。
scikit-learnのPCAのソースコードを見てみると、fitの中身でやっていることはscipyのlinalg.svd、つまりSVD(Singular Value Decompotision : 特異値分解)であることがわかります。
特異値分解の理解には線形代数、特に行列の理解が不可欠です。行列の復習についてはこちらの記事にまとめました。今回出てきた特異値分解の理解を助けるような構成で書いていますので、よくわからない方は要チェックです。
参考記事 : データサイエンスに必須な高校数学・大学数学の基礎知識を一瞬で復習しつつ特異値分解を理解する【行列・ベクトル・線型代数】
参考ドキュメント : scipy | scipy.linalg.svd
より主成分分析の理解を深めるために 〜 PCAの属性 Attributes を調べる
scikit learnのPCAの理解を深めるために、フィッティングされたPCAインスタンスpcaの属性を調べてみます。scikit learnの属性は最後にアンダーバー_がついているもので、フィッティングしたときにインスタンスに格納される値です。
pca.components_
# array([[ 0.00405128, -0.00116205, 0.0152752 , 0.99987444],
# [-0.30848927, 0.09044334, -0.94678621, 0.01581922]])
pca.n_components_ # 2
pca.n_features_ # 4
components_は特徴空間における主成分軸で、データの分散が最大となる方向を表しています。特異値分解で言うところの右特異ベクトルです。
サイズは(n_components_,n_features_)の配列です。つまり、列は主成分の数(今回はハイパーパラメータで2とセットしたので2)、行は訓練データであるペンギンの特徴量の数です。
pca.n_samples_ # 342
これは訓練データXのサンプル数(行数)です。
pca.mean_ # array([ 43.92192982, 17.15116959, 200.91520468, 4201.75438596])
# X.mean(axis=0)
これはXの平均と一致します。
pca.explained_variance_ # array([6.43292592e+05, 5.15448141e+01])
pca.explained_variance_ratio_ # array([9.99891315e-01, 8.01178384e-05])
explained_variance_は特異値の分散です。次の式で確認できます。ここからが面白いです。
X = X - np.mean(X, axis=0) # 分散の計算のため、全サンプル平均で引いておく
u, s, vh = np.linalg.svd(X) # SVD:特異値分解
n_samples, n_features = X.shape
explained_variance_ = (s ** 2) / (n_samples - 1)
explained_variance_
# array([6.43292592e+05, 5.15448141e+01, 1.60356408e+01, 2.34349326e+00])
sはXの特異値ベクトルでした。(特異値分解の記事参照。) 特異値の分散とは、この各成分の2乗をサンプル数-1(今回は342-1=341)で除したものです。(ということは、正確には分散ではなく不偏標本分散ですね。)
そのうち、先頭2つがpca.explained_variance_と一致していることがわかります。今回セットした主成分軸が2なので、2つ出てきているのですね。
ちなみに、右特異ベクトルの先頭2つvh[:2]を見てみると、次のような中身です。
array([[ 0.00405128, -0.00116205, 0.0152752 , 0.99987444],
[-0.30848927, 0.09044334, -0.94678621, 0.01581922]])
これはまさに最初に見たcomponentsの中身ですね。つまりcomponentsの中身が右特異ベクトルであるということも確認できました。
こうやって紐解いていくと、scikit learnで実行する「魔法の一文」も、中身は高校や大学で学んだ数学が元になっているんだなーと実感します。数学って凄い。
pca.singular_values_ # array([14810.90050885, 132.57745515])
これは上で出てきたsの上位2つと一致します。つまり選択された主成分の特異値ベクトル。
sの中身を見てみると
array([14810.90050885, 132.57745515, 73.94696412, 28.26890873])
なので、量が大きい順に並んでいることがわかります。いかにも主成分っぽさがわかります。
ちなみにこのsの1個目、第一主成分は4つある成分のうち何%を占めているのかを調べてみます。
s[0]/s.sum() # 0.9843946493570583
きゅ、98%...
主成分の固有値の割合が「寄与率」と呼ばれていて、上から8割くらいの軸を選べればまあヨシみたいな風潮がありますので、98%というのは過剰な気がします。
と、ここまで来て実はデータセット正規化したほうがよいのでは...ということに気付きました。正規化した場合どうなるかは、次の次の章で実践してみます。
最後はnoise_variance_です。
pca.noise_variance_ # 9.18956701291344
ノイズの分散という意味ですが、これはexplained_variance_[2:].mean()と一致します。つまり、特異ベクトルのうち、選択した軸以外の分散の平均となります。
これが要はノイズ成分ということで、この分は主成分分析の結果(選択した2軸)から除外されてしまいますので、小さい方が好ましいですね。
参考ドキュメント : scikit learn | sklearn.decomposition.PCA
より主成分分析の理解を深めるために 〜 PCAのメソッドを調べる
続いてscikit learnのPCAのメソッドを調べてみます。ここでようやく、主成分分析とは何で、特異値分解とは何の役に立つのかというのが理解できる気がします。
メソッドはインスタンスからドット.をつけて呼び出す関数です。fitは上にも書いたように特異値分解でモデルをフィッティングしました。他にはどんなものがあるのでしょうか。
一番重要なのがtransformです。上で結果をプロットしたときに使いました。
pca.transform(X)
# array([[-4.52023209e+02, 1.33366364e+01],
# [-4.01949980e+02, 9.15269401e+00],
# [-9.51740904e+02, -8.26147557e+00],
# ...
#
pca.transform(X).shape # (342, 2) つまりサンプル数 × 主成分の数
このメソッドの入力は訓練データでありペンギンの特徴行列であるXです。ここでは、Xに対してある計算をすることで、ペンギンの特徴行列を主成分軸の空間(今回は2軸なので平面)へ変換(射影)を行っています。
その計算が何かというと、こちら。
u[:,:2]*s[:2]
# array([[-4.52023209e+02, 1.33366364e+01],
# [-4.01949980e+02, 9.15269401e+00],
# [-9.51740904e+02, -8.26147557e+00],
# ...
たしかに一致してそうですね。スライスしている2は主成分の数で、は左特異ベクトルに特異値を掛けたものです。
ちなみに元のサイズはこちら。
u.shape # (342, 342)
s.shape # (4,)
は対角行列でした。そのうち、最も分散の大きい上位2つの軸(特異値)を、元のXから取り出した形になっています。これが特異値分解を使った主成分分析の意味っぽいです。
参考ドキュメント : scikit learn | sklearn.decomposition.PCA
データセットを正規化して主成分分析してみる
というわけで先程の途中で発覚した「実は正規化したほうがいいんじゃない説」を試してみます。
感覚的にはそれもそのはずで、特にペンギンの「体重」はくちばしやフリッパーの長さに対して数値が大きい分、分散も大きくなるので、何かしら影響が大きく出そうですよね。
今回は「平均値で引いて、標準偏差で割る」という形で試してみます。(ちなみに、単純に「最大値で割る」という形でも、似たような結果になります)
# Normalize
XN = (X-X.mean())/X.std() # 平均で引いて標準偏差で割る。
# 以降は上で実践した流れと同じ。
pcaN = PCA(n_components=2)
pcaN.fit(XN)
XN_2D = pcaN.transform(XN)
df['PCAN1'] = XN_2D[:,0]
df['PCAN2'] = XN_2D[:,1]
sns.lmplot('PCAN1','PCAN2',hue='species',data=df,fit_reg=False)
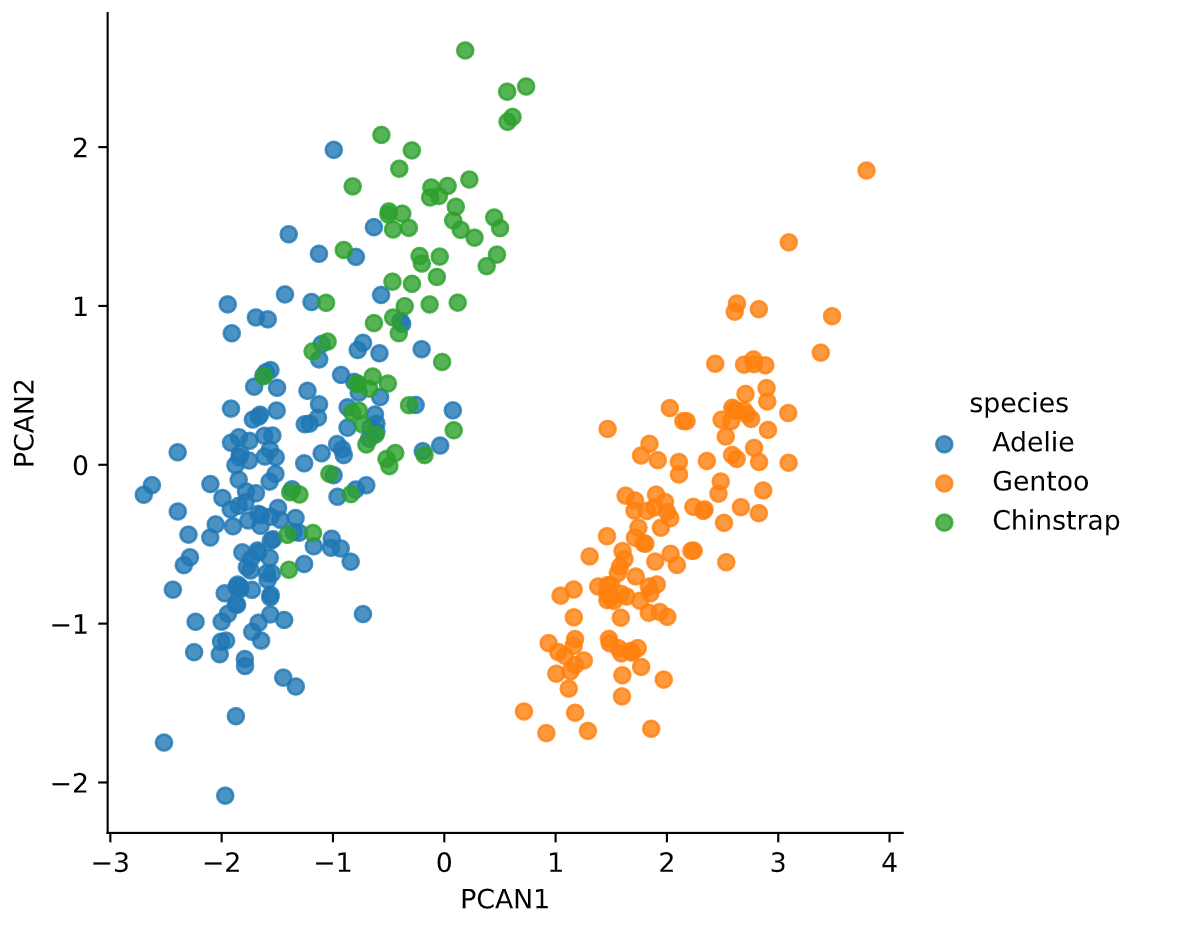
う〜ん、いまいち。正規化しない方が、青と緑がより分離できていた気がします。
寄与率も調べてみます。
XN_ = XN - np.mean(XN, axis=0)
uN, sN, vhN = np.linalg.svd(XN_)
sN/sN.sum() # 寄与率
# array([0.4779364 , 0.25314036, 0.17405808, 0.09486516])
ああ、こっちはそれっぽい。第一主成分の寄与率が47%で、第二主成分までの累積寄与率が73%です。ということは第三主成分まで入れないと、正規化した場合はイマイチそうですね。
主成分分析の白色化 whitening
実は主成分分析には白色化(whitening)という便利な前処理があります。
それを使ってやってみても、変数間のスケールが統一されて正規化した場合と似たような結果になります。ぜひお試しください。
白色化には、PCAのハイパーパラメータとしてwhiten=Trueを指定します。
pcaW = PCA(n_components=2,whiten=True)
pcaW.fit(X)
XW_2D = pcaW.transform(X)
実は、特徴的な軸を選ぶのにもっと簡単でわかりやすい方法がある。
と、ここまでかなり複雑で線形代数を駆使した「主成分分析」なる手法を見てきましたが、プロットしてみるとイマイチでしたよね。
そこで、以前書いた特徴行列の可視化編の記事を一度振り返っていただきたいのですが、実はペアプロットもっとそれっぽく種類を分類できている2軸があることにお気づきになられると思います。
しかも、すでにある軸から選べるということは、イコールとても解釈しやすいし、説明しやすいのです。このペンギンのペアプロットを見れば、「体重」と「くちばしの長さ」の2つの特徴がわかれば、大体どのペンギンの種類なのかが主成分分析をしなくてもわかりそうですよね。うん、わかりやすい。
主成分分析で新しくできる軸はあくまで「主成分1」「主成分2」で、それが一体ペンギンの何を意味する特徴なのか、解釈するのは分析者に委ねられています。
なので、「2軸で表したい!ならば主成分分析だ!」ではなく、まずペアプロットで特徴的な変数がないかな?と調べてみたほうが幸せになれるかもしれません。
まとめ
というわけで、今回はペンギンデータセットとscikit-learnを使って、ペンギンの4軸の特徴を主成分分析し、新しい2軸の平面でペンギンの種類を表現してみました。機械学習の分類では「教師なし学習」と呼ばれる問題です。基本的な流れは前回取り扱った回帰問題と同じでした。
また、主成分分析(PCA)の理解を深めるために、中で動いている特異値分解(SVD)にまで踏み込み、NumPyのライブラリを使ってPCAと同じ計算を行ってみました。
最後にちょっと触れたように、主成分分析は万能ではないので、まずはペアプロットでデータの特徴をつかむのも大事です!
今後もペンギンデータセットを使って他の問題やモデルについても取り扱っていこうと思います。
それでは〜
今回使った機械学習プログラム全文 〜 主成分分析・PCA
最後に、今回使ったPythonプログラムのコードをまとめておきます。実行文は、たったの10行でした。
# データセットの準備
y = df.species # 目的配列
X = df.drop('species', axis=1) # 特徴行列
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 主成分分析で2軸を選択する
pca.fit(X) # 中で特異値分解する
X_2D = pca.transform(X) # 訓練データを2軸に変換する
df['PCA1'] = X_2D[:,0] # 変換した2軸をデータフレームに追加する
df['PCA2'] = X_2D[:,1] # 同上
import seaborn as sns # 目的配列を色分けとして、可視化する
sns.lmplot('PCA1','PCA2',hue='species',data=df,fit_reg=False)


