データサイエンティストスキルチェックリストに出てくる用語の意味を調べてみた ~ データサイエンス力基礎数学統計数理基礎2

2022-01-06

データサイエンティスト協会なるところが「データサイエンティストスキルチェックリスト」なる資料を公開しているので、勉強がてら用語の意味をまとめています。自分であれこれ調べて自分なりにまとめていきたいと思います。

ボリュームがかなり多いので何回かに記事を分ける予定です。

まとめ記事はこちら : 【まとめ記事】データサイエンティストスキルチェックリストの用語の意味を調べてみる【データサイエンス】

今回は「データサイエンス力基礎数学統計数理基礎」編その2。

この記事を読んでいけばデータサイエンティストという人材に求められている知識の片鱗がわかったり、データサイエンティストと名乗る人たちの会話に役立つかもしれません。何かのご参考に。

データサイエンティストスキルチェックリストとは？

こちらの記事をご参考に。

【まとめ記事】データサイエンティストスキルチェックリストの用語の意味を調べてみる【データサイエンス】

他のカテゴリの用語まとめ記事にも上のページから飛べます。

それでは以下にデータサイエンス力「統計数理基礎」に出てくる用語の意味を調べていきます〜

相関関係と因果関係 - correlation / causality

相関関係とは２つの事柄に関連性があること。因果関係とはある事柄を原因として別の事柄が変化すること。

因果関係は相関関係の一部ですが、相関関係が因果関係とは言い切れないです。相関関係は「原因と結果」とは限らず、あくまで関連性の「傾向」に過ぎません。

たとえば「ペンギンの羽の長さが長いほど、体重が重い傾向がある」といったことがわかった場合、これは相関関係と言えますが、因果関係ではないですよね。「羽が長いので、体重が重い」とは限りません。羽が長いペンギンほど、身長も高くて、体が大きいので体重が重い、という「傾向」はなんとなくありそうです。しかし、羽が長いことが原因で、必ず体重が重くなるとは言い切れません。~~食べ過ぎと運動不足が原因で、めっちゃ腹が出てるかもしれない。~~

この違いを正しく理解しないと、「データから価値を創り出す」というデータサイエンスの本質からずれた結論を導いてしまう恐れがあるので注意です。というか日常生活でも情報弱者になり不安を煽って広告費を稼ぐ目的の低質なメディアに踊らされ貴重な人生の時間を無駄にします

尺度水準 - scales of measurement

下に行くほど高い水準で、高い水準は低い水準の性質を含みます。

名義尺度 - nominal scale

区別できる名称。 血液型(A,B,O等のラベル)、住所など。

順序尺度 - ordinal scale

順番や大小関係に意味があるが、間隔に意味がない尺度。 順位、級など。間隔に意味がないので、3位 - 1位 = 2位とはならない。

間隔尺度 - interval scale

0に意味がなく、等間隔で間隔に意味がある尺度。 比率に意味がない。西暦、気温など。間隔に意味があるので引き算して「体温が1度下がった」とは言えるけれど、比率に意味がないので「体温が2%下がった」とは言わない。

比例尺度 - ratio scale

0が原点で、間隔と比率に意味がある尺度。 身長、体重、時間、速度など。間隔だけでなく、「体重10%増」などと比率が言える。

統計WEB | 変数の尺度

ピアソンの相関係数 - Pearson correlation coefficient

２つの確率変数X,Yがどれくらい似ているか？を表す統計量。共分散÷標準偏差の積。「そーかん」ってよく言われるヤツは数式で言うとコレ。

範囲は-1以上1以下で、-1に近いほど「負の相関が強い」(逆の方向に増減する)、1に近いほど「正の相関が強い」(同じ方向に増減する)と言われる。0に近いと「相関がない」、つまり2つの変数に関連性が低いということ。

r_{xy} = \frac { \displaystyle \sum_{i = 1}^n (x_i - \overline{x}) (y_i - \overline{y}) } { \sqrt{ \displaystyle \sum_{i = 1}^n (x_i - \overline{x})^2} \sqrt{ \displaystyle \sum_{i = 1}^n (y_i - \overline{y})^2} }

もしくは

r_{xy} = \frac { {\displaystyle \frac{\displaystyle \sum_{i = 1}^n (x_i - \overline{x}) (y_i - \overline{y}) }{n} } } { \sqrt{\displaystyle \frac{ {\displaystyle \sum_{i = 1}^n (x_i - \overline{x})^2}}{n}} \sqrt{\displaystyle \frac{ {\displaystyle \sum_{i = 1}^n (y_i - \overline{y})^2}}{n}} } = \frac{s_{xy}}{s_xs_y}

分子は「XとYの共分散（偏差の積和の平均）」で、分母は「XとYの標準偏差の積」になっています。

式を見ると確かに、 $x$ と $y$ がそれぞれ平均に対して逆の動きを取れば符号がマイナスになるし、似たような動きをしていれば(一緒に平均から遠ざかるように動いていれば)、分子の絶対値が大きくなりそうですね。全体のばらつき(標準偏差)で割っているので、範囲が-1から1に収まるのも納得です。

ちなみに、ピアソンの積率相関係数とも言います。

確率分布 - probability distribution

確率変数がとる値を横軸に、その確率を縦軸においた分布のこと。 変数がサイコロのように値が飛び飛びだと「離散型」、重さなど連続した値をとる場合は「連続型」といいます。

こちらの過去記事でグラフ付きで色々書いてます。統計学のまとめ - 確率分布編【Pythonでグラフ化あり】

二項分布 - binominal distribution

結果が2種類のイベントの成功確率が従う確率分布のこと。

コインの裏表のような2種類の結果から片方が起こる確率 $p$ とし。 $n$ 回の試行でそれが発生する回数(=確率変数 $X$ )が $x$ になる確率は、

P = {}_n\mathrm{C}_xp^x(1 - p)^{n - x}

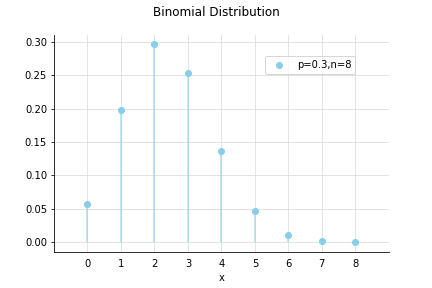
期待値と分散は以下のようになります。

E(X) = np

V(X) = np(1 - p)

ちなみに、このような飛び飛びの確率変数に対しての発生確率を確率質量といい、これを表現する関数を正規分布のような確率密度関数に対して確率質量関数といいます。

二項分布のサンプル数 $n$ が増えていくと、 $np = \lambda$ という一定値で考えられるようになり、ポアソン分布になります。

ポアソン分布 - poisson distribution

「ある期間に平均 $\lambda$ 回起こるイベント」の発生回数の確率分布。

f(x) = \frac{e^{-\lambda}\lambda^x}{x!}

平均と分散はどちらも $\lambda$ 。

時間あたりのwebアクセス数などのモデル化に使えます。例えば、1時間のPV(ページビュー)が平均10回の記事が、ある1時間にx回アクセスされる可能性はどれくらいあるのか？という確率の分布は以下のようになります。

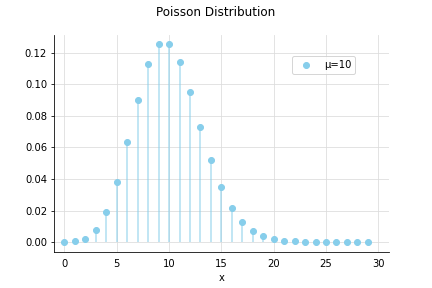
$\lambda$ を大きくしていくほど、山の中心が右側にずれていくとともに、裾野が広がって(平均以外の発生確率の割合が増えて)いきます。

統計WEB【用語】ポアソン分布

統計WEB ポアソン分布

クラメールの連関係数 - Cramer's coefficient of association

量的変数の相関はピアソンの相関係数を使うのに対し、質的変数の関係の強さ(相関)を求めるのに使う方法。

たとえば「ペンギンカフェの客の性別と注文するメニューに相関はあるか？」といった問題について、客の「性別」を縦軸、「注文したメニュー」を横軸とした表を作り、そのマスにあてはまる数(サンプル数)を書き込んで客の動向を集計してみます。(このような表をクロス集計表と言います。)

クラメールの連関係数は以下の式で表せます。カイ二乗値÷サンプル総数 $n$ ÷クロス集計表の行列(r×c)のうち小さい方-1、の平方根です。0~1の値をとり、1に近いほど相関が強いと言えます。

V = \sqrt{\frac{\chi^2}{n \times \min (r-1,c-1)}}

カイ二乗値は以下の手順で求めます。

クロス集計表の各マスのサンプル数からそのマスの期待度数を引く。期待度数は、「そのマスと同じ行のサンプル数合計×そのマスと同じ列のサンプル数合計÷全サンプル数 $n$ 」。
1で求めた値(サンプル数-期待度数)の二乗を、それぞれのマスの期待度数で割る。
表内の2で求めた値をすべて足して合計値を求める。

このように求めた合計値が $\chi^2$ です。これでクロス集計表に対して行と列の連関係数が求められ、質的変数に対しても相関の強さが求められます。

指数関数 - exponential function

$a\gt0$ で $a\neq1$ となる $a$ に対して $a^x$ で表せる関数のこと。 この定数 $a$ を「底」と言う。

自然指数関数は「ネイピア数」 $e=2.718...$ を底とする。多くの場合特に何も言われなければこの自然指数関数を指します。 $e^x$ のことを $\exp(x)$ という書き方もしますね。

対数関数(log関数) - logarithm function

底 $b$ を「何乗したら $x$ になるか」を $\log_{b}x$ と表したものが対数で、その変換を関数のように表現したもの。 $\log(x)$ のように書く。

対数の定義は、 $b^{\log_bx}=x$ が成り立つこと。特に底がネイピア数 $e$ の場合を自然対数(natural logarithm, $\ln$ )、工学でよく使う底が10の場合は常用対数(common logarithm, $\lg$ )、情報理論でよく使う底が2の場合は2進対数(binary logarithm, $lb$ )という。 $\ln$ で書かれた対数を見たことある気がするけど、自然対数のnaturalを意味するnだったんですね。

自然対数関数は指数関数と逆の関係にあるため、 $\ln(\exp(x))=x$ であり、 $\exp(\ln(x))=x$ です。

データが指数関数的に増えていく場合、グラフの軸を「対数軸」でとるとプロットが直線的になりデータが見やすくなります。このとき、一方の軸が対数軸のグラフを片対数グラフ(semilog)、両方の軸が対数軸のグラフを両対数グラフ(log-log)と言います。軸の目盛りが「1,10,100,...」と等間隔に増えていたら、「あ、これ対数グラフだな」と気付けます。

まとめ

というわけで、今回はデータサイエンティスト協会が公開している「データサイエンススキルチェックリスト」「基礎数学」「統計数理基礎」に出てくる用語の意味をまとめてみました。

「基礎数学」ということで、やはりデータサイエンスに数学は欠かせないということですね。理系の時代来てる。

他のカテゴリもまとめて行く予定です。ぜひご参考に。

まとめ記事はこちら : 【まとめ記事】データサイエンティストスキルチェックリストの用語の意味を調べてみる【データサイエンス】

それでは〜

統計学のまとめ - 確率分布編【Pythonでグラフ化あり】

ペンギンデータセットでデータサイエンス入門〜機械学習の基本・単回帰編【Python/scikit-learn/教師あり学習】

ペンギンデータセットで機械学習/データサイエンスをはじめよう〜ダウンロード編

【オススメ】未経験からプログラマーへ転職できる【GEEK JOBキャンプ】

▼ Amazonオススメ商品

ディスプレイライトデスクライト BenQ ScreenBar モニター掛け式

スマートLEDフロアライト間接照明 Alexa/Google Home対応

データサイエンティストスキルチェックリストに出てくる用語の意味を調べてみた ~ データサイエンス力基礎数学統計数理基礎2

目次

データサイエンティストスキルチェックリストとは？

相関関係と因果関係 - correlation / causality