統計学のまとめ - 確率分布編 【Pythonでグラフ化あり】

こんにちは。

先日ブログで数式が書けるようになったのでウッキウキで数式を扱おうと思い至り、まずは統計の基礎をまとめておくページを作ろうと思いました。

今回は第2弾の確率分布編です。

忘れかけたらこのページを参照して思い出せるように書きたいと思います。

基礎統計量

基礎統計量についての説明はこちらの記事を御覧ください。

Pythonでプロットする準備

今回はグラフで視覚的に見たほうがイメージしやすいかと思い、PythonのMatplotlibで視覚化します。

パッケージの準備。予めpip installしておきます。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats

SciPyの詳細な使い方はこちらのドキュメントで。

様々な数学・統計に使えるライブラリが提供されているOSSで、数式をスクラッチせずにプログラムが記述できます。

確率分布 - Probability distribution

確率変数がとる値を横軸に、その確率を縦軸においた分布のこと。

変数がさいころのように値が飛び飛びだと「離散型」、重さなど連続した値をとる場合は「連続型」という。

確率変数 - Random variable

「ある変数$x$をとる確率$p$」が存在する変数$X$のこと。

期待値 - Expected value

確率変数の期待値は、$X$が取りうる値$x$に対してそれぞれの確率$p$の積を合計して求める。

離散型の場合は合計$\sum$、連続型の場合は積分$\int$を使う。

確率密度関数 - Probability Density Function

連続型の場合、ある一点をとる確率は0になってしまうので、確率密度($X$の相対的な出やすさ)を使い、これを関数で表したもの$f(x)$を確率密度関数という。

この場合、確率は一点ではなく範囲で求める必要がある。

また、確率密度関数は必ず以下の条件を満たす。

正規分布 - Normal Distribution

自然界に多く現れる代表的な分布。ガウス分布ともいう。

平均は$\mu$で分散は$\sigma^2$。

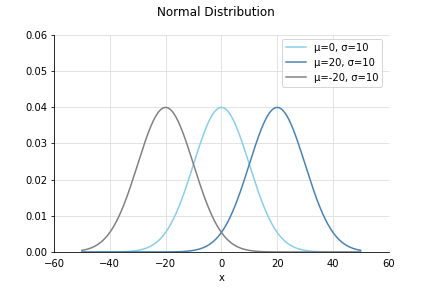
$\mu$が山の中心になっていることがわかりますね。

以下、グラフ化に使ったPythonコードです。

colors = ['skyblue','steelblue','grey']

mu = [0,20,-20] # mean
sd = 10 # standard deviation

X = np.arange(-50,50,0.1)

fig = plt.figure(figsize=(6, 4), facecolor='white')
fig.suptitle('Normal Distribution')

ax = fig.add_subplot(111,xlabel='x', ylabel='')

for i,m in enumerate(mu):
  # ここで正規分布を作成
  Y = scipy.stats.norm.pdf(X, loc=m, scale=sd)
  ax.plot(X, Y, c=colors[i], label=f"μ={m}, σ={sd}", zorder=10)

ax.tick_params(bottom=False)

ax.set_xlim(-60,60)
ax.set_ylim(0,.06)
ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)
ax.legend(bbox_to_anchor=(.98,.98), loc='upper right', borderaxespad=0)
[ax.spines[side].set_visible(False) for side in ['right','top']]

scypy.stats.normは正規分布を、pdfはProbability Density Functionの略で、確率密度関数を呼び出せます。

locで平均を、scaleで標準偏差を指定できます。

より詳しい使い方はこちら SciPy.Org - scipy.stats.norm

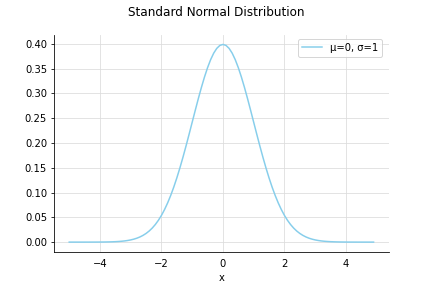
標準正規分布 - Standard normal distribution

正規分布のうち、平均が0で分散が1のもの。

mu = 0 # mean
sd = 1 # standard deviation

X = np.arange(-5,5,.1)
Y = scipy.stats.norm.pdf(X, loc=mu, scale=sd) # 標準正規分布

fig = plt.figure(figsize=(6, 4), facecolor='white')
fig.suptitle('Standard Normal Distribution')

ax = fig.add_subplot(111,xlabel='x', ylabel='')
ax.plot(X, Y, c=colors[0], label=f"μ=0, σ=1", zorder=10)

ax.tick_params(bottom=False)
ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)
ax.legend(bbox_to_anchor=(.98,.98), loc='upper right', borderaxespad=0)
[ax.spines[side].set_visible(False) for side in ['right','top']]

二項分布 - Binomial distribution

離散型の代表的な分布。

コインの裏表のような2種類の結果から片方が起こる確率$p$とする。

$n$回の試行でそれが発生する回数(=確率変数)$X$が$x$になる確率は、

この確率分布を二項分布という。

期待値と分散は以下の通り。

このような飛び飛びの確率変数に対しての発生確率を確率質量といい、これを表現する関数を正規分布のような確率密度関数に対して確率質量関数といいます。

確率質量関数はPlobalility Mass Functionの略で、SciPyのpmfというメソッドで呼びます。

以下ではポケモンのゲームを例にして、一撃必殺技「ぜったいれいど」(成功率30%)を8回使って成功回数ごとの確率の分布を調べてみました。

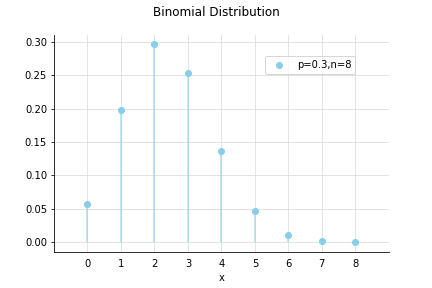
成功回数が2回である確率が最も高いですね。せいぜい1~3回くらいしか成功しなさそうなことがわかります。

p = 0.3 # 成功確率
n = 8 # 試行回数
k = np.arange(0, n+1) # 成功回数
Y = scipy.stats.binom.pmf(k, n, p)

fig = plt.figure(figsize=(6, 4), facecolor='white')
fig.suptitle('Binomial Distribution')

ax = fig.add_subplot(111,xlabel='x', ylabel='')
ax.plot(k, Y, 'bo', c=c, label=f"p={p},n={n}", zorder=10)
plt.vlines(k, 0, Y, colors=c, lw=2, alpha=0.5)

ax.set_xlim(-1,n+1)
ax.tick_params(bottom=False)
ax.set_xticks(np.arange(0,n+1,1))
ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)
ax.legend(bbox_to_anchor=(.9,.9), loc='upper right', borderaxespad=0)
[ax.spines[side].set_visible(False) for side in ['right','top']]

SciPy.org - scipy.stats.binom

ポアソン分布 - Poisson distribution

二項分布で$n$が非常に大きく$p$が非常に稀な場合の分布。

このとき、$np = \lambda$という一定値で考えられる。

逆に、「ある期間に起こる事象の平均回数」として、$\lambda$をパラメータとして与える。

平均と分散はどちらも$\lambda$。

時間あたりのwebアクセス数などのモデル化に使えます。

例えば、1時間のPV(ページビュー)が平均10回の記事が、ある1時間にx回アクセスされる可能性はどれくらいあるのか？という確率の分布は以下のようになります。

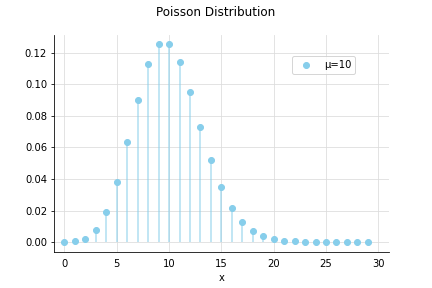
最も多いのは10回(約12%)ですが、4%くらいの確率で15回アクセスされたり、5回しかアクセスされない、といったこともありそうです。

逆に20回見られたり、1回も見られない、ということは起こり得なさそうですね。何らかの外的要因で、バズったり、サーバーに不具合が起きていることを疑ったほうがよさそうです。

mu = 10 # 平均の発生回数。(上の式のλに相当)
n = 30 # 調べたい回数(横軸)の上限

X = np.arange(0,n,1)
Y = scipy.stats.poisson.pmf(X,mu,loc=0)

fig = plt.figure(figsize=(6, 4), facecolor='white')
fig.suptitle('Poisson Distribution')

ax = fig.add_subplot(111,xlabel='x', ylabel='')
ax.plot(X, Y, 'bo', c=c, label=f"μ={mu}", zorder=10)
plt.vlines(X, 0, Y, colors=c, lw=2, alpha=0.5)

ax.set_xlim(-1,n+1)
ax.tick_params(bottom=False)
ax.set_xticks(np.arange(0,n+1,5))
ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)
ax.legend(bbox_to_anchor=(.9,.9), loc='upper right', borderaxespad=0)
[ax.spines[side].set_visible(False) for side in ['right','top']]

$\lambda$を大きくしていくほど、山の中心が右側にずれていくとともに、裾野が広がって(平均以外の発生確率の割合が増えて)いきます。

統計WEB【用語】 ポアソン分布

統計WEB ポアソン分布

SciPy.org - scipy.stats.poisson

その他の分布

そのうち追加していきます。

参考

BellCurve 統計WEB https://bellcurve.jp/statistics/

Qiita 1. Pythonで学ぶ統計学　2. 確率分布[scipy.stats徹底理解]