データサイエンティスト スキルチェックリストに出てくる用語の意味を調べてみた ~ データサイエンス力 基礎数学 統計数理基礎1
目次
こんにちは。
データサイエンスを勉強している一般人です。
データサイエンティスト協会なるところが「データサイエンティストスキルチェックリスト」なる資料を公開しているので、勉強がてら用語の意味をまとめています。自分であれこれ調べて自分なりにまとめていきたいと思います。
ボリュームがかなり多いので何回かに記事を分ける予定です。
まとめ記事はこちら : 【まとめ記事】 データサイエンティスト スキルチェックリストの用語の意味を調べてみる 【データサイエンス】
今回は「データサイエンス力 基礎数学 統計数理基礎」編その1。数がめっちゃ多いので何回か分けます。
この記事を読んでいけばデータサイエンティストという人材に求められている知識の片鱗がわかったり、データサイエンティストと名乗る人たちの会話に役立つかもしれません。何かのご参考に。
データサイエンティスト スキルチェックリストとは?
こちらの記事をご参考に。
【まとめ記事】 データサイエンティスト スキルチェックリストの用語の意味を調べてみる 【データサイエンス】
他のカテゴリの用語まとめ記事にも上のページから飛べます。
それでは以下に データサイエンス力 「統計数理基礎」 に出てくる用語の意味を調べていきます〜
順列 - permutation / 組み合わせ - combination
区別できるモノの集合から一定数を抜き出して作れるパターンの数。順番を考慮するのが順列、考慮しないのが組み合わせ。
なんか中学くらいで習ったことあるけどあんまり覚えてないアレ。
純烈順列は4人の男性から3人選んで1列に並べるパターンの数。は「4×3×2」で24通り。
組み合わせは4人の男性から3人選ぶ組み合わせで、順番はどうでもいい。は「(4×3×2)/(3×2×1)」で4通り。「選ばれない人の組み合わせ」と同義なので、でも同じ。
ちなみに組み合わせはGoogle検索で計算可能。Googleで「4 choose 3」と検索してみよう〜
条件付き確率 - conditional probability
「あるイベントBが発生した」とすでにわかっている条件のもとで、「別のあるイベントAが発生」する確率のこと。「Bが発生し、かつAも発生する確率」÷「Bが発生する確率」で計算できます。
例えば、とある町のカフェ「ペンギンカフェ」の来店履歴から、次のことがわかっているとします。「客の5%に37度以上の熱があった。そのうち20%がウィルスに罹っていた。」さて、この確率が今後変わらないと仮定して、今来た客に熱があるようです。この客がウィルスに罹っている可能性は何%でしょう?みたいな問題。
普通に考えて答えは20%ですが、これを一般化して書くと次のようになります。
- が「熱がある客が来るイベント」で、発生確率
- が「熱がある客がウィルスに罹っている」イベントで、発生確率
- は「AND」で確率の場合は掛け算で計算できます。
- が条件付き確率で、が発生した条件下でが起きた確率、つまり「熱がある客が来て、その客がウィルスに罹っている確率」と言い換えられます。
- 計算すると「0.05 × 0.20 / 0.05」で 20%となります。
参考 : 統計用語集 | 条件付き確率
「え、それが何...?」という感じかもしれませんが、機械学習のアルゴリズムで使われる「ベイズの定理」や統計的推論における「最尤法」で必要となります。
期待値 - expected value
確率変数のとる値すべてに、それぞれの発生確率をかけたものの合計。
サイコロという「1,2,3,4,5,6」の6パターンの値がランダムで発生するシステムを考えます。すべて発生確率は1/6です。
このシステムから出る値は確率に基づくため確率変数と呼ぶことが出来ます。「のとる値すべて」に「それぞれの発生確率」をかけて「合計」してみます。
というわけで「期待値は3.5」と言えます。言わずもがな。
一般化するとこう。確率が一様の場合は、値の合計をで割ることになるので、つまり平均値と一致します。
参考 : 統計用語集 | 期待値
独立 - independence
確率で発生する2つのイベントに対して、片方のイベントがもう片方のイベントに影響を与えない関係のこと。
1個のサイコロの出目の1回目と2回目、もしくは2個のサイコロの出目みたいな関係のことです。
イベントとが独立である場合、期待値について以下の式が成り立ちます。
参考 : 統計用語集 | 独立
よく似た言葉に「排反事象」がありますが、「排反」はサイコロの出目の1と2のように、「1回の試行で同時に起こらない、別のイベント」のことを指します。排反は事象(イベント)に対して言う言葉で、独立は「試行」に対して使う言葉です。
分散 - variance
たくさんあるデータの分布の広がり具合、つまり「ばらつき」を表す量。 ばらつきが大きいほど大きな値になる。単位は元のデータの単位の二乗になります。
求め方は、偏差(各データの、全データ平均値との差)を二乗して全部足して、データのサンプル数で割る。二乗する理由は、平均との差がマイナスでもプラスでも同様に「どれくらい離れているか」を表したいから。サンプル数で割る理由は、サンプル数に依存しない値にしたいから。(値が大きいほどばらつきが大きい、という指標が欲しいのに、サンプル数によって値が増えてしまうと目的が達成できない。)
標本分散の場合はで、母分散(population variance)を特にと表記するのが一般的なようです。
また、確率変数と母平均を使うと、分散を次のようにも表現できます。
また、とが独立であれば以下の式が成り立ちます。
標準偏差 - standard deviation
分散の正の平方根のこと。√分散。 分散と同じく、値が大きいほど「ばらつきが大きい」を示す量。
分散は単位が元の二乗になってしまうため、足したり引いたり比べたりができませんが、標準偏差ならできます。
を使うのは実際のデータのサンプル(標本)からわかる標準偏差、を使うのは真(母集団)の標準偏差です。分散と同様。
四分位数 - quartile / パーセンタイル - percentile
値が小さい方からデータを並べて、サンプル数で4等分した区切りの位置にある値のこと。
25パーセンタイル(第一四分位数)、50パーセンタイル(=中央値、第二四分位数)、75パーセンタイル(第三四分位数)といった言い方をする。
よく「箱ひげ図」というグラフで使われます。第1〜第3の範囲(四分位範囲と言う)を「箱」、中央値を箱の中の「線」、箱の外から最小値・最大値までを「ヒゲ」のように線を伸ばして描きます。(平均を使う、10%で区切る、など他の区切り方もあります。)
箱ひげ図はデータの分布、つまり偏り方や範囲について、複数の集団における違い(よくあるのは時間的な推移)を一つのグラフで表したいときに便利です。
母平均 - population mean
母集団の平均のこと。 。対して「標本平均」と言うと母集団の中から取り出した限られたサンプル(標本)の平均値のことです。
母平均は統計で推定したい未知の値です。このような未知の値を「母数」と言います。
「コウテイペンギンの身長の平均値は?」なんて言われても正確にこの世のすべてのペンギンを調べて答えられる人はいないですよね。なので「1000羽くらい調べて平均ということにしちゃえ」と適当なサンプルを抽出して平均を計算するしかないのです。このようなサンプルを用いて求めた平均が標本平均。誰も知らない「この世のすべてのコウテイペンギン集団」、いわゆる「母集団」の平均値が「母平均」です。統計的に推定するしかありません。
ちなみに「母分散」なども同じ考え方で、母集団の分散のことです。
不偏分散 - unbiased variance
期待値が母分散と一致する推定量。 標本分散にをかけて少し大きくしたもの。
標本分散は一致推定量ですが、不偏推定量ではなく、サンプル数が大きくない場合は期待値が母分散より小さくなります。
ん?いきなり何言っちゃってんのって感じですが、「推定量」つまり母数をそれっぽく推定する量には、以下の条件を満たしてもらう必要があるようです。
- 一致性(consistency)
- サンプルサイズが大きくなるほど推定量が母数に近づく性質。
- 不偏性(unbiasedness)
- サンプルサイズに依らず、推定量の期待値が母数に一致する性質。
参考 : 統計WEB | 推定量の性質
要は、闇雲な値を推定量としても意味がないので、「確率的に最も期待できる値(期待値)は母分散と一致させたい」、「けれども標本の分散に対してをかけないと期待値が母分散に一致しない!」「じゃあそれを不偏性のある分散=不偏分散と呼んで母分散の推定にはこっちの値を使おう!」ということみたいです。
証明の計算は長いので省きますが、例えばサンプル数が30だとすると、「30/29」(>1)を掛けて標本分散より「ほんの少し大きい値」にして、「母数の分散を推定したい場合はこっち(不偏分散)を使え!」ということなんですね。実際の母集団よりもサンプルデータは数が少ないので、多少大きく見積もる(実際はもう少し大きくばらついているだろう)というのは、なんとなく感覚的にはわかる気がします。
参考 : 統計WEB | 標本分散と不偏分散
「不偏分散の期待値」と「母分散」が一致する計算は以下のリンクにありましたので、ここでは割愛します。
参考 : 【2通りの証明】不偏分散はなぜn-1で割るのか?【推測統計の重要ポイント】
標準正規分布 - standard normal distribution
平均は0, 分散は1になる正規分布のこと。
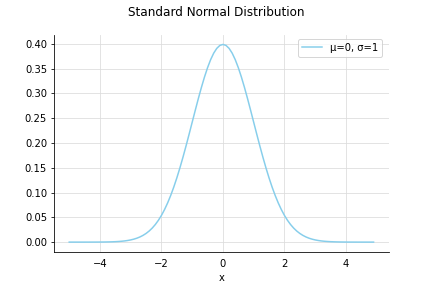
ちなみに、こちらの過去記事でPythonでプロットする方法を書いています。
統計学のまとめ - 確率分布編 【Pythonでグラフ化あり】
一般化された正規分布はこっちの式。自然界に多く現れる代表的な分布で、ガウス分布ともいいます。
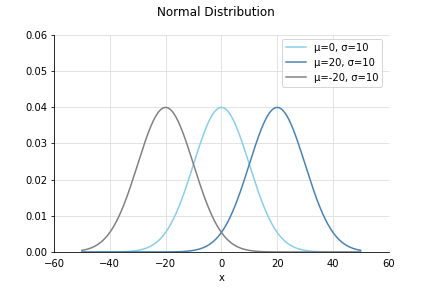
平均と分散によって形を変えます。平均とばらつき、という意味を考えるとそうなっていて当たり前ですね。を山の中心とした左右対称の分布です。
まとめ
というわけで、今回はデータサイエンティスト協会が公開している「データサイエンス スキルチェックリスト」「基礎数学」「統計数理基礎」に出てくる用語の意味をまとめてみました。
「基礎数学」ということで、やはりデータサイエンスに数学は欠かせないということですね。理系の時代来てる。
他のカテゴリもまとめて行く予定です。ぜひご参考に。
まとめ記事はこちら : 【まとめ記事】 データサイエンティスト スキルチェックリストの用語の意味を調べてみる 【データサイエンス】
それでは〜
関連記事
統計学のまとめ - 確率分布編 【Pythonでグラフ化あり】
ペンギンデータセットでデータサイエンス入門 〜 機械学習の基本・単回帰編【Python/scikit-learn/教師あり学習】


