Pythonで正規分布のグラフを描く方法を解説【初心者向け/サンプルコード】

こんにちは。

今回はPythonで正規分布のグラフを描く方法をまとめます。

一般的にはScipyなど統計に便利なPythonライブラリを使うと思いますが、今回は自分で分布の数式を書いてグラフ化することも試してみます。

Python初心者向けに、簡単な解説も付記します。

必要なパッケージのインストール

後半で解説する「数式を書いてグラフにする方法」では、scipyは不要です。

$ pip install numpy matplotlib scipy

正規分布とは

自然界に多く現れる代表的な分布。ガウス分布ともいいます。

連続的な値をとる「何か」の発生数が、平均(期待値)が最も多く、平均に対して左右対称にばらつく様子を表すモデルとして使われます。平均値・中央値・最頻値は一致します。

「何か」とは例えば「同じ種類の大人ペンギンの身長」とかです。100羽、1000羽、と大量にサンプルをとっていくと、横軸を身長として、その身長にあてはまるペンギンの数は正規分布のような形になります。(多分。)

正規分布の数式

正規分布の確率密度関数は以下のように表されます。

平均は$\mu$で分散は$\sigma^2$です。

確率分布の期待値は$\mu$になります。

正規分布のグラフ

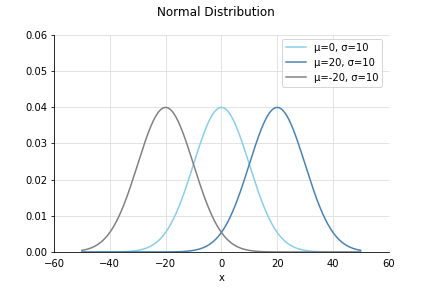
$\mu$が山の中心になっていることがわかりますね。

Pythonで正規分布のグラフを描くコード

以下、グラフ化に使ったPythonコードです。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats

colors = ['skyblue','steelblue','grey']

mu = [0,20,-20] # mean
sd = 10 # standard deviation

X = np.arange(-50,50,0.1)

fig = plt.figure(figsize=(6, 4), facecolor='white')
fig.suptitle('Normal Distribution')

ax = fig.add_subplot(111,xlabel='x', ylabel='')

for i,m in enumerate(mu):
  # ここで正規分布を作成
  Y = scipy.stats.norm.pdf(X, loc=m, scale=sd)
  ax.plot(X, Y, c=colors[i], label=f"μ={m}, σ={sd}", zorder=10)

ax.tick_params(bottom=False)

ax.set_xlim(-60,60)
ax.set_ylim(0,.06)
ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)
ax.legend(bbox_to_anchor=(.98,.98), loc='upper right', borderaxespad=0)
[ax.spines[side].set_visible(False) for side in ['right','top']]

真ん中より少し下でYに代入している行を解説すると、scypy.stats.normは正規分布を、pdfはProbability Density Functionの略で、確率密度関数を呼び出せすメソッドです。

引数の配列Xに対する確率密度関数を返します。Xはx軸に相当する等差数列です。また、locで分布の平均を、scaleで標準偏差を指定します。

より詳しい使い方はこちら SciPy.Org - scipy.stats.norm

for文でmuの中身を一つずつ取り出して、平均値の異なる3つの正規分布をプロットしています。

サンプルコードの他の部分は、グラフに必要な部分です。

Scipyを使わずに、正規分布の数式を書いてグラフにする方法

さて、Scipyを使うことでYに正規分布を作成することができましたが、数式がわかっていればScipyを使わなくても正規分布を作れそうなので、実際に試してみます。

ライブラリを増やしたくない、増やせないといった場合にも使えますが、何より自分で書くことでより理解が深まりそうです。

先程、正規分布の式が以下のようになると書きました。

これをPythonで記述します。

サンプルコード

import numpy as np
import matplotlib.pyplot as plt

mu = 0  # mean
sd = 10 # standard deviation

X = np.arange(-50,50,0.1) # x軸 0.1ステップ

# 正規分布の式を再現
Y = (
  np.exp(-((X-mu)**2 / (2*sd**2)))
  /
  np.sqrt(2*np.pi*sd**2)
)

# プロット
fig = plt.figure(figsize=(6, 4), facecolor='white') # 図形サイズと背景色
fig.suptitle('Normal Distribution') # タイトル

ax = fig.add_subplot(111,xlabel='x', ylabel='') # サブプロットの位置と軸ラベルをセット

ax.plot(X, Y, c='steelblue', label=f"μ={mu}, σ={sd}", zorder=10) # axにプロット

ax.tick_params(bottom=False) # 下側(x軸)の目盛りを非表示

ax.set_xlim(-50,50) # x軸の範囲
ax.set_ylim(0,.05) # y軸の範囲
ax.grid(axis='x', c='gainsboro', zorder=9) # 縦グリッドの色指定・プロットより背面にセット
ax.grid(axis='y', c='gainsboro', zorder=9) # 横グリッドの色指定・プロットより背面にセット

ax.legend(bbox_to_anchor=(.98,.98), loc='upper right', borderaxespad=0) # 凡例の位置
[ax.spines[side].set_visible(False) for side in ['right','top']] # 右・上の枠線を非表示

解説

Yに代入している箇所に注目すると、今度はscipy.statsではなく数式を書いています。$\exp()$の部分を、$\sqrt{2\pi \sigma^2}$で割るように書いていますが、数式の意味は上に書いた正規分布の関数式と同じであることがわかると思います。

長い数式を見やすくするために全体を()で囲って中身を改行していますが、一行で書いてもOKです。

他の部分は主にMatplotlibのグラフの設定です。コメントで簡単に各行の目的を書いておきました。

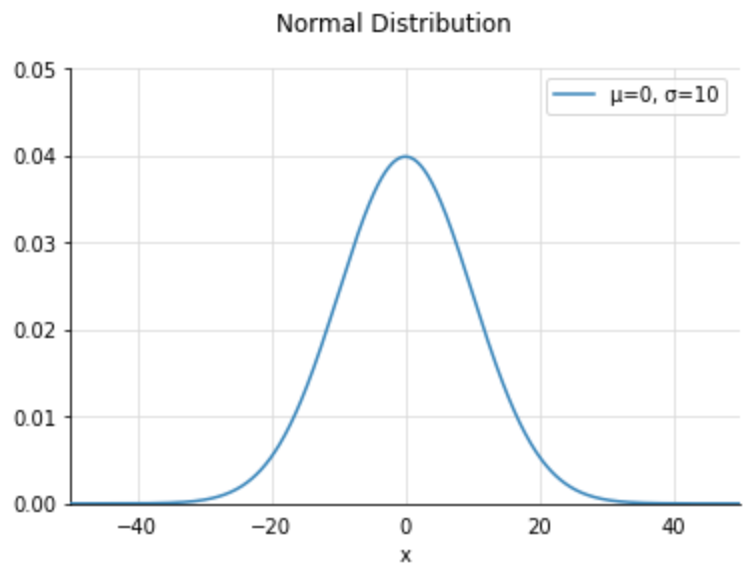
プロット結果

scipy.stats同様にプロットできることが確認できました。

まとめ

というわけで今回はPythonで正規分布のグラフを作る方法をまとめました。

Scipyを使わなくても自分で数式を書くことで同じグラフを作成できます。Pythonライブラリを使うと便利ですが、数式の理解を深めたい場合は、自分で書いてみるのも良さそうです。

他の確率分布のグラフ化についても以下の記事でまとめています。

統計学のまとめ - 確率分布編 【Pythonでグラフ化あり】