【データサイエンス入門】決定木分析をPythonで簡単に試す & 分類と条件分岐を可視化する方法まとめ【サンプルコードあり】
目次
こんにちは。大晦日も暇なのでひたすら勉強です。
今回は巷でよく聞く「決定木」とは何なのかをまとめるとともに、Pythonで実際にプログラムを書いて動かしてみたいと思います。
結果を直感的に理解しやすいのが決定木の良いところです。可視化する方法も2種類まとめてみます。
決定木とは
決定木は機械学習のアルゴリズムの一つで、木の枝分かれのように条件分岐を行ってデータを分類していくことができます。このアルゴリズムによって得られる分類結果は、「どのような条件で分類が行われたか」がわかりやすいため、分類の意味を理解するのに便利な手法です。
たとえば動物の種類を「種族は?」「空を飛べる?」「体長はどれくらい?」といったような質問形式の条件で分類されるイメージです。用意するデータは「特徴量」と、答えとなる「ラベル」(ここでは動物の種類)を持つ教師データがあればOK。与えられたデータセットに対して「分類にベストな質問」は、なんと決定木アルゴリズムがデータから勝手に推定してくれます。これが機械学習の強みですね。
機械学習とは何か、分類とは何か、といったような基本的な解説は以下の記事でもご紹介しています。簡単な「分類」問題を機械学習プログラムで解いています。scikit-learnを使った分類問題の参考にどうぞ。こちらの記事ではガウシアンナイーブベイズという手法を使っています。ぜひ今回の記事と合わせて御覧ください。
ペンギンデータセットでデータサイエンス入門 〜 教師あり学習・分類編【Python/scikit-learn/機械学習/ガウシアンナイーブベイズ】
【前提】 Pythonと使用ライブラリのバージョン情報
それでは実際にPythonプログラムで決定木分析を試していきたいと思います。
以下は私の動作確認したバージョン情報です。
- Python
- 3.10.1
- matplotlib
- 3.5.1
- pandas
- 1.3.5
- scikit-learn
- 1.0.2
データセットの準備
今回の教師データも例によってこのブログで頻出のペンギンデータセットを使います。ダウンロードと前処理方法は以下の記事で。
必要なライブラリと上記で用意したデータセットをインポートします。
import pandas as pd
import numpy as np
df = pd.read_csv('penguins.csv') # ペンギンデータセットの読み込み
df = df.rename(columns={ # 列名の変更
'bill_length_mm' : 'bill_length',
'flipper_length_mm' : 'flipper_length',
})
df = df[['species','flipper_length','bill_length']] # 必要な列だけ取り出す
df = df[~df.isnull().any(axis=1)] # Nullがある行を削除
今回はペンギンの羽の長さflipper_lengthとくちばしの長さbill_lengthから、ペンギンの種類speciesを予測するという分類問題に取り組んでみます。
説明変数(特徴量)Xと目的変数(分類するラベル)yは以下のようにセットします。
X = df.drop(columns='species').values
y = df['species']
Pythonで決定木のモデルを作成する方法
決定木にはscikit-learnという機械学習ライブラリの、DecisionTreeClassifierというモデルを使用します。
scikit-learnを使った機械学習の流れは以下の記事で解説しています。
決定木の場合も上の記事と同様に、「モデル選択 → モデルのインスタンス化とパラメータの選択 → 特徴行列と目的配列の設定 → フィッティング」といった流れで書いていきます。
from sklearn.tree import DecisionTreeClassifier # モデル選択
tree = DecisionTreeClassifier() # モデルのインスタンス化、パラメータ設定
tree.fit(X,y) # 特徴行列と目的配列の設定、フィッティング
Pythonで作成した決定木のモデルを活用する方法 〜 未知のデータを分類する
先程フィッティングして作成したモデルが、正しくペンギンの種類を分類できるかテストしてみます。
feature_names = ['flipper_length','bill_length'] # 特徴量の名前
x1 = df[feature_names].values[:3] # テスト用に先頭から3サンプルの特徴量ベクトルを抽出
tree.predict(X1) # フィッティングしたモデルインスタンスに特徴量ベクトルを入力し、ペンギンの種類を予測
# 結果 : array(['Adelie', 'Adelie', 'Adelie'], dtype=object)
分類した結果はすべてAdelieとなり、元の先頭3サンプルのデータもすべて「アデリーペンギン」だったので、正しく分類できました。
なるほど、分類できる決定木が確かに作れたようだ!とは思うものの、決定木と言えば学習したモデルによる「分類がそれっぽくできていること」を「見た目」で確認したいですよね。
というわけで、続いて「決定木分析を可視化する方法」についてまとめていきます。
Pythonで決定木を可視化する方法1. 分類を「塗りつぶし等高線」で平面上に色分けする ~ matplotlib.pyplot.contourf
データがどのように分類されるのか、平面上で見てみます。
はじめに色分けのための前処理として、ペンギンの種類を数値(0,1,2)に変換します。
species = df.species.unique() # ユニーク値の配列を作成
species_number_map = { species[i] : i for i in range(len(species)) } # ユニーク値ごとに数字を割り当てた辞書を作成
species_number_map # {'Adelie': 0, 'Gentoo': 1, 'Chinstrap': 2}
y = df.species.map(species_number_map) # マッピング
今回はこの0,1,2の数値を目的変数yとします。
以下のプログラムで平面上に決定木による分類を可視化します。等高線を塗りつぶすmatplotlib.pyplot.contourfで実現できます。
import matplotlib.pyplot as plt
model = DecisionTreeClassifier() #
cmap = 'winter' # カラーマップの指定
# データを散布図でプロット
ax = plt.gca()
ax.scatter(X[:,0],X[:,1], c=y, s=30, cmap=cmap, clim=(y.min(),y.max()),zorder=3)
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# フィッティング
model.fit(X,y)
# 予測
xx,yy = np.meshgrid( # 軸の下限・上限内に格子点(メッシュグリッド)を作成
np.linspace(*xlim, num=200), # *は要素取り出しで、xlim[0],xlim[1] と同じ。
np.linspace(*ylim, num=200)
)
Z = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape) # 格子点全てに対してフィッティングしたモデルで分類予測
# 結果を塗りつぶし等高線でプロット
n_classes = len(np.unique(y)) # 目的変数のユニーク値の数 = 3
contours = ax.contourf( # contourはcontour line(等高線), fはfill(塗りつぶし)
xx, yy, Z, alpha=0.3, # 格子上(xx,yy)に予測結果Zをプロット
levels=np.arange(n_classes + 1) - 0.5,
cmap = cmap, clim=(y.min(),y.max()), zorder=1
)
ax.set(xlim=xlim, ylim=ylim)
出力結果
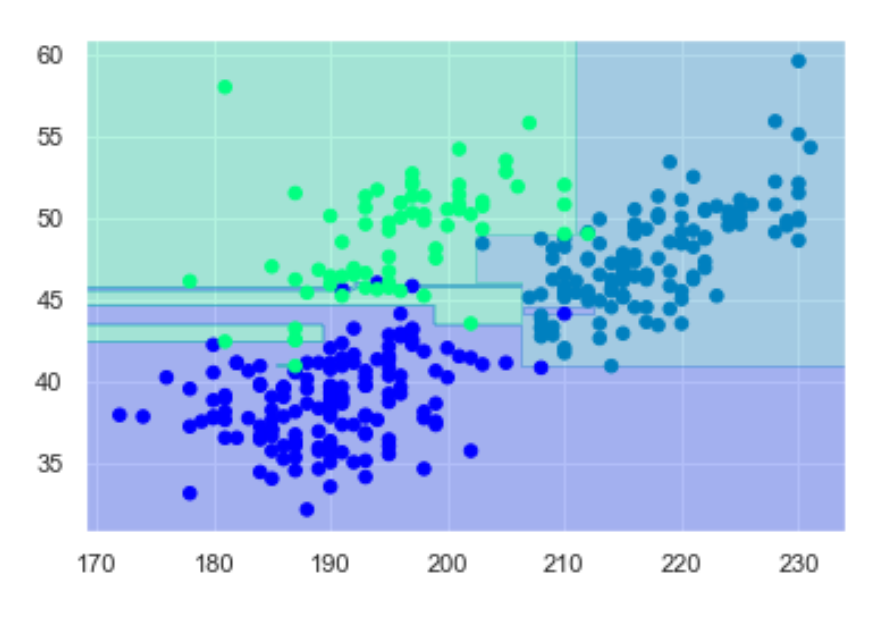
無事、平面上にペンギンの種類を色分けできました。散布図のような点がモデルのフィッティングに使用したペンギンのデータ(教師データ)、塗りつぶされているエリアが「決定木モデルによって平面内格子点の分類を予測した結果」です。
つまり、未知のペンギンの「羽の長さ」と「くちばしの長さ」がわかれば、この図に当てはめることで「どの種類(色)のペンギンか」が予測できるようになりました。
ただ、色塗りのエリアに細い線のような場所があるので、少し過剰にフィッティングしてる感が否めないですね。このように簡単に過学習を起こしてしまうのが決定木のデメリットです。
決定木の「枝の深さ」をハイパーパラメータmax_depthで設定できるので、どこまで細かく分類させるかはモデルをフィッティングする前に変更できます。
tree = DecisionTreeClassifier(max_depth=3) # 枝分かれ回数を「3回まで」にする
プログラムの補足説明
np.ravel()は、配列を一次元化します。np.c_[a,b]は配列aとbを結合します。一次元配列同士だと、二次元配列になります。contourfのlevelsは等高線の高さで、色分けするためには分類される値(0,1,2)が間に入るよう設定します。以下にプログラム内の設定値の背景を補足します。
n_classes # 3 ... 分類結果(0,1,2)の数
np.arange(n_classes) # array([0, 1, 2])
np.arange(n_classes+1) # array([0, 1, 2, 3])
np.arange(n_classes+1)-0.5 # array([-0.5, 0.5, 1.5, 2.5])
これで分類結果(0,1,2)が等高線の間に入り、すべて綺麗に色分けできるようになります。
参考資料
カラーマップはこちらのサイトからお好きなものを選べます。 matplotlib | Choosing Colormaps in Matplotlib
cocntourfの詳細についてはこちらのドキュメントに詳しい使い方が書いてあります。 matplotlib | matplotlib.pyplot.contourf
Pythonで決定木を可視化する方法2. 条件分岐の枝分かれの様子を描く ~ sklearn.tree.plot_tree
「決定木なんだから木の形をしていてほしい!」
ということで決定木らしく条件分岐の様子を枝分かれする木の枝葉のように描画する方法をご紹介します。
from sklearn.tree import plot_tree # plot_treeのインポート
tree = DecisionTreeClassifier(max_depth=3) # インスタンスの作成、枝分かれは3回まで
tree.fit(X,y) # フィッティング
plt.figure(figsize=(15,10)) # あまり小さすぎると文字が読めないので適当なサイズにする
plot_tree(tree, feature_names=feature_names, filled=True) # 条件分岐の枝分かれを描画
plt.show()
先程の塗り分けのような難しいポイントはなく、シンプルで簡単なプログラムで書けます。
出力結果
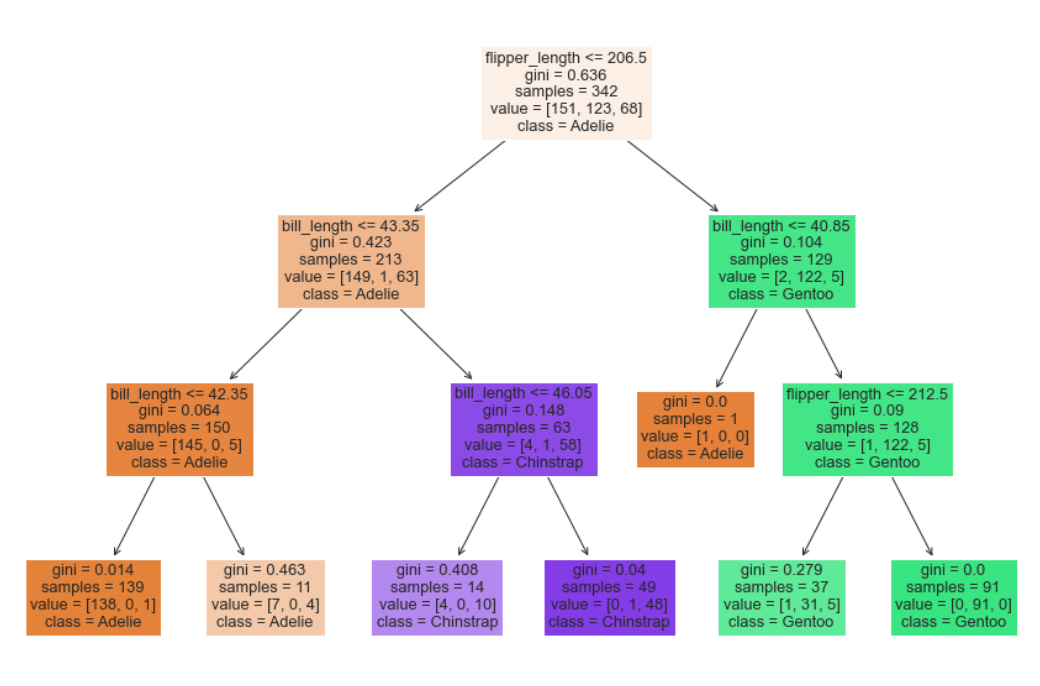
そうそう、これよこれ。これが決定木よね。
箱の中に「木が分岐する条件」と「サンプル数」、「ジニ係数」、「サンプルの分類結果」が書かれています。条件がTrueのサンプルは、左側に進んでいきます。「羽の長さが206.5mm以下で、くちばしの長さが43.35mm以下で、...」といった感じですね。
枝分かれでどのようにサンプルデータが分類されていったかが、とてもわかりやすくなりました。
決定木分析の「ジニ係数」とは
決定木の「ジニ係数」とは分類における「不純度」、つまり違うものが混ざっている割合を元に算出される係数です。0~1までの値をとり、0に近いほど純粋、1に近いほど不純となります。
以下の計算式で計算されます。
ここでは分類されるクラスの数、は分類の不純度で「その条件で各値が分類される確率」です。実際に上の出力結果における最初の条件分岐で計算してみます。
1 - ( np.power(151/342,2) + np.power(123/342,2) + np.power(68/342,2) )
# 結果 : 0.6361786532608323
各分類の確率を二乗した合計を、1から引きました。上の図でもgini = 0.636なので同じ値が出ましたね。ジニ係数は0に近いほど純粋なので、この時点ではかなり汚い分類状態といえます。(最初の箱は分類前なので、汚くて当然ですね。)
ちなみに、決定木とは「枝分かれによって分割前後のジニ係数の差が最大となる条件」、つまり「最も綺麗に分類できるような条件」を探して分類条件を決めていくアルゴリズムのようです。
まとめ
というわけで今回は決定木分析をPythonで簡単に試す方法と、決定木分析による分類と枝分かれの様子を可視化する方法についてまとめてみました。
非常に簡単で高速に分類でき、わかりやすい結果を得られる一方、過学習を起こしやすいというデメリットもありました。
今回のようなPyhtonを使った分析手法をPythonの基礎からわかりやすくまとまっている書籍をご紹介します。Pythonを使ってデータサイエンスに取り組みたい方はぜひ最初に読んでおきたい必読書だと思います。
Pythonデータサイエンスハンドブック ―Jupyter、NumPy、pandas、Matplotlib、scikit-learnを使ったデータ分析、機械学習
ご参考になれば幸いです。
それでは〜。



