Pythonで正弦波の作成&FFTによる周波数解析と可視化する方法

こんにちは。

時系列データの統計処理をPyhtonでやってみたいと思い、これから色々まとめてみようと思います。

今回はPythonで正弦波の作成と、その波を周波数解析してプロットしてみます。

正弦波とは

時間によって周期的に振幅が変化する波の基本。

たしか高校数学で習ったやつ。今回はこれを使います。

$A$が振幅、$f$が周波数、$t$が時間です。

Pythonで簡単な波形データを作ってみる

上で書いた正弦波を作る前に、簡単な波形データを作って練習してみます。

まず最初に必要なライブラリをインポートします。

import matplotlib.pyplot as plt
import numpy as np

ホワイトノイズ

ランダム雑音とも。

t = 100  #データ長
mean = 0.0  #平均値
std  = 1.0  #分散

y = np.random.normal(mean,std,t)

plt.plot(y)
plt.show()

正弦波

サインカーブとも。

# x軸 : 0~2piまで100個に等分した等差数列
x = np.linspace(0, 2*np.pi, 100)

y = np.sin(x)

plt.plot(x,y)
plt.show()

なるほどです。波が表示されました。

周波数を指定して正弦波を作成する

適当な正弦波は上のように作れますが、今回はFFTで周波数解析を行うのが目的です。

なので、解析結果が正しく得られているか確認できるように、あらかじめ周波数を決めた正弦波を作ります。

この数式をプログラムで再現して正弦波を作ってみます。

今回は5kHz、つまり5000Hzの波を作ってみます。(音にするとワリと甲高い音。)

sec = 0.01 # [sec]
f = 5000 # [Hz]
N = 100000  # データ点数
A = 1 # 振幅

t = np.linspace(0, sec, N)

y = A*np.sin(2*np.pi*f*t)

tは0.01秒刻みの時間軸です。

yは上の数式そのままです。

np.と書くことでNumpyのメソッドを呼び出して使っています。

作成した正弦波をFFTで周波数解析する

FFTは高速フーリエ変換という手法のことで、離散フーリエ変換を効率よく計算するアルゴリズムです。

要はデジタルの波形データを素早く周波数解析できます。

つまり、「時系列データが、どの周期(周波数)の特徴を持っているか？」を簡単に調べることができます。

細かい理論はここでは割愛しますが、Python、というかNumpyではnp.fft.fftを使うとベクトルデータをFFTしてくれます。詳しくはNumpyのドキュメントで。

書いてみるとこう。

yf = np.fft.fft(y,N)

たった一行。簡単。

どんなデータになったか見てみると...

何コレ。

ということでもう少し続きます。

FFTしたデータの縦軸(レベル)を見やすくする

np.fft.fftのままだと解釈が難しかったりデータが見にくかったりするので少しお手当します。

まず縦軸の変換です。

ayf = np.abs(yf[1:int(N/2)])
dayf = 20*np.log10(ayf)
dayf = dayf - max(dayf)

1行目のスライスで2つのことを行っています。

1. データの前半半分を取り出す
2. 低周波の直流成分(バイアス)をカット

ナイキスト周波数(サンプリング周波数の半分)で結果が折り返されるため、データの後半は前半部分の鏡の結果になります。(先程可視化したときに両側に棒が立っていた理由です。)

つまり、データの後半部分は解析には不要なため、削除します。

2は必ずしも必要ではない(特に今回は自作データなのでなくてもいい)ので0から始めてもよいのですが、一応1からスライスを始めます。

また、周波数解析の縦軸はパワースペクトルといって絶対値の2乗を対数軸で見ることが一般的です。

np.absで絶対値にしてから、2乗して、$10\log_{10}$でdB(デシベル)に変換します。dBは電気・工学系のデータを比で扱うときによく用いられる単位です。

真数を二乗するので、頭の10は2をかけて20にしています。

最後の行で、縦軸はデータのピークを基準0として表現したいので、ベクトルデータの全値と最大値の差をとってベクトルを更新しています。

FFTしたデータの横軸(周波数)を見やすくする

見やすくというかわかりやすく。こちらは1行です。

xf = np.arange(1/sec, N/2/sec, 1/sec)

np.arangeの使い方は(start, stop, step)です。

stopは含まれません。

FFTはデータ点数分の結果が返ってきます。これを、波形生成したときの時間を使って周波数ステップに変換します。

時間$t$[sec]と周波数$f$[Hz]の単位は逆数の関係で、$f = 1/t$ で変換できます。

先程データのレベル変換の際に[1:int(N/2)]のデータを抽出したことに気をつけて、プロットするデータと横軸のデータの数が一致するようにしましょう。(一致しないと、プロットするときにエラーが出ます。)

作成した波形データと周波数解析結果を可視化する

それではデータを可視化して、意図通りの波形データ作成と周波数解析ができているかを確認してみます。

せっかくなので、1つのグラフに波形と周波数解析結果を載せてみます。

グラフパラメータの設定。

title = f'{f}Hz wave form & spectrum'
xlabel = ['Time[sec]','Frequency[Hz]']
ylabel = ['Amplitude','Level[dB]']
xmin = [0,0]
xmax = [0.001, 20*1000] # 波形は0.001秒、周波数は20kHzまで
ymin = [-1, -120]
ymax = [1, 5]

Matplotlibでグラフ作成。

fig = plt.figure(figsize=(12, 4), facecolor='white')
fig.suptitle(title)

# waveform -----------------
ax = fig.add_subplot(121,xlabel=xlabel[0], ylabel=ylabel[0])
ax.plot(t, y, c='black', zorder=10)

ax.set_xlim(xmin[0],xmax[0])
ax.set_ylim(ymin[0],ymax[0])

ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)

# fft ----------------------
ax = fig.add_subplot(122,xlabel=xlabel[1], ylabel=ylabel[1])
ax.plot(xf, dayf, c='black', zorder=10)

ax.set_xlim(xmin[1],xmax[1])
ax.set_ylim(ymin[1],ymax[1])

ax.grid(axis='x', c='gainsboro', zorder=9)
ax.grid(axis='y', c='gainsboro', zorder=9)

出力されたグラフはこちら。

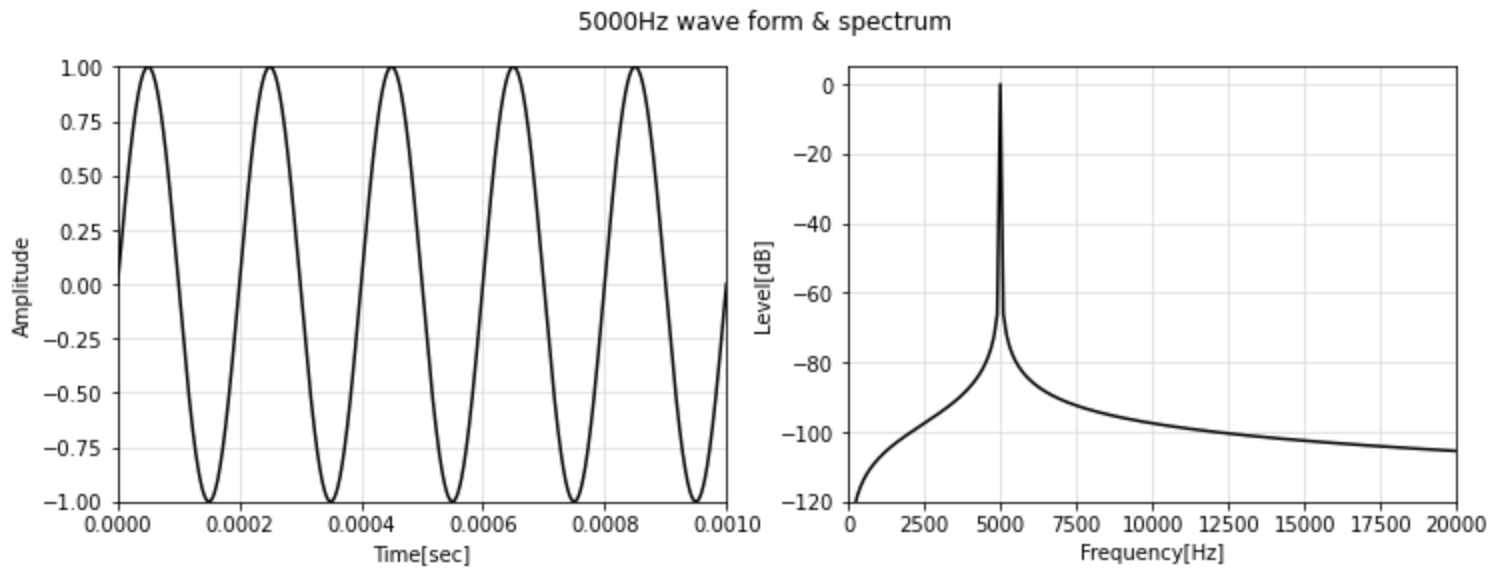
左のグラフを見ると、1/1000秒に5個の波があるので、1秒間に5000個の波があるということで、狙い通り5000Hzの波が作成できています。

右のグラフを見ると、横軸の目盛りが5000Hzのところにピークがあるので、FFTによる解析もうまくいっていそうです。

y軸の最小値を-60dBあたりに設定ですれば、更にそれっぽく見えそうです。

まとめ

ということで、今回はPythonとNumpyを使って以下のことを試しました。

• 周波数を指定した正弦波の時系列データの作成
• FFTで周波数解析
• FFTの結果(縦軸・横軸)を見やすく変換する方法
• 波形データと周波数解析結果の可視化
• 作成した時系列データでFFTがうまくできているか確認

ご参考に。

それではー。